 PID控制
PID控制
PID 的非系统学习是博主以平衡小车控制为项目进行的
# 原理
原理的方面,请参考这篇文章吧:
着重强调一个方面:对于 P 控制的补偿,为什么有的时候永远无法到达预定值?
以无人机的高度控制为例:当发现误差值为某个值,乘以系数
之后,此时的升力被设定为了飞机的重力,此时整个系统被迫达到了稳态,从而无法升高
# 公式
# 一般式
其中:
为本次的误差值, 为上次的误差值,以此类推 为三种方式的系数,需要在实验中确定
# 增量式
取
这个就是增量式,对于速度的 PID 控制有时会用到它
# 注意的量
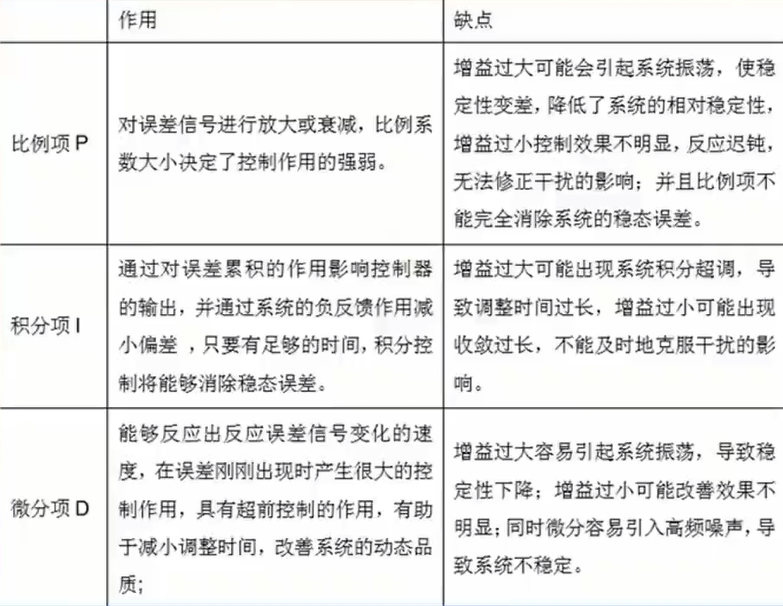
# 实例
在微控制器上的信条
由于微控制器性能有限,所以有以下准则:
- 使用做差代替微分
- 使用累加代替积分
# 位置控制
对于位置控制,我们使用的就是刚刚讲到的全部 PID 形态

# 代码实现
int Position_PID(int Encoder, int Target)
{
static float Bias, PWM, Integral_bias, Last_bias;
// 计算此次误差
Bias = Encoder - Target;
// 计算历次误差的积分
Integral_bias += Bias;
// 计算此次算出的 PWM
PWM = Position_KP * Bias + Position_KI * Integral_bias + Position_KD * (Bias - Last_bias);
// 保留此次误差
Last_bias = Bias;
return PWM;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
这是最简单的实现方式,输入的两个量此次系统反馈回来的状态值与系统设定的目标值。通过计算将我们应该设定的 PWM 值计算出来。随后将此值给到定时器设定 PWM
考虑到 PWM 对于我们系统稳态的稳定性,我们应该将 PWM 算法放进一个定时器中断中以确保实时计算
# 技巧
位置控制的调节经验可以总结为:先只使用 P 控制,增大 P 系数至系统震荡之后加入微分控制以增大阻尼,消除震荡之后再根据系统对响应和静差等的具体要求,调节 P 和 I 参数
# 速度控制
对于速度的控制,我们只是使用 PI,而且使用了增量式的控制方式。故公式可简化为:
注意:是变化量!
# 代码实现
int Speed_PI(int Encoder, int Target)
{
static float Bias, PWM, Last_bias;
// 计算此次误差
Bias = Encoder - Target;
// 计算此次算出的 PWM
PWM += Speed_KP * (Bias _ Last_bias) + Speed_KI * Bias;
// 保留此次误差
Last_bias = Bias;
return PWM;
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
需要注意的代码方面的东西基本与位置控制一致
编辑 (opens new window)
上次更新: 2020/11/10, 10:11:00
