加速度计

加速度计的本质

加速度计的本质是测量力！测量力！测量力！

上面的本质对于你理解为什么在使用陀螺仪与加速度计进行姿态解算的时候为什么会出现误差，我们接下来来探讨一下：

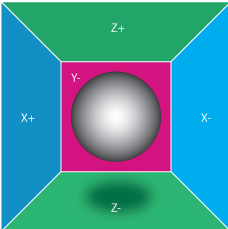
这是一个加速度计的简易模型，我们是通过物体在具有加速度时击打在每个壁上的力推算得到的三个轴上的加速度

关于倾角测量的理想

聪明的你一定猜到了可以使用测量到的加速度大小来表示物体此时倾角的大小：

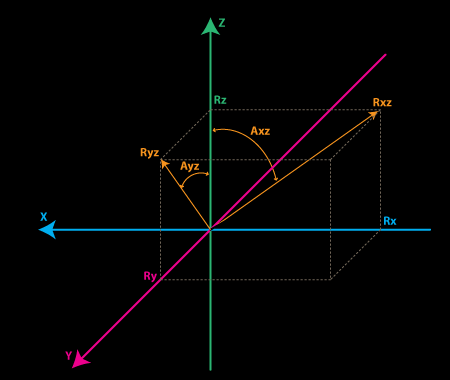
例如这样一个物体的状态：

• R 是三个方向上的合加速度；
•  是向量 R 分别在 X、Y、Z 轴上的投影；
•  是向量 R 在 XZ 平面上的投影；
•  是向量 R 在 YZ 平面上的投影；
•  是  和  之间的夹角；
•  是  和  之间的夹角；

所以根据勾股定律：

通过三角函数的反函数：

但是准确的事实真的是这样吗？

关于倾角测量的现实

我们来看这样一个情况：

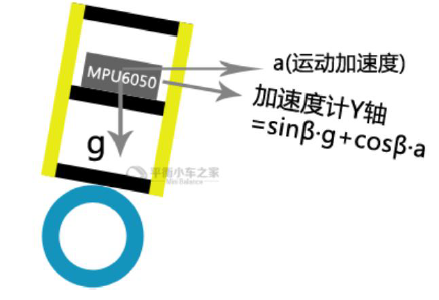
如果真的可以测量角度的情况下是这样的：

也就是在 Y 轴上的加速度只是重力加速度的分量的时候才可以准确的计算倾角，但是实际情况下，请牢记加速度传感器的本质是测量力，所以小车的整体加速度在传感器安装处的体现 a 对加速度计在 Y 轴上测量到的加速度产生了影响：

且这个体现 a 的大小具体为：

为小车的车轮加速度，而 是小车车体的角加速度， 为加速度计的安装高度，二者的叠加加速度导致了欲使用加速度测量值衡量倾角的误差

回到数据本身

回到 MPU-6050 传感器中，我们已经分别读取到 3 个轴的加速度数据，但是我们读到的加速度数字量的单位还不是 。最后的转换，我们还需要引入加速度传感器的灵敏度（Sensitivity），单位通常是 。

比方说，加速度传感器的灵敏度 。灵敏度值可以在加速度传感器规格书中找到。要获得最后的单位为  的加速度，我们使用下列公式计算：

陀螺仪

陀螺仪测量的是角速度的值，很高兴我们可以通过角速度的积分来获得一个大致的倾角值（是的，今天就是要和倾角杠到底！）

关于倾角测量的理想

假定 Angle_X 是我们想要测的在 X 轴的倾角，而 Gyro_X 是从陀螺仪上得到的角速度值

每 5ms 执行以下语句：

Angle_X = Angle_X + Gyro_X * 0.005;

通过离散的积分运算叠加得到了倾角的值。

关于倾角测量的现实

但是由于从陀螺仪测量的角速度获得角度信息，经过积分运算。如果角速度信号存在微小的偏差和漂移，比如在传感器静止的情况下，输出不为零。经过积分运算之后，变化形成积累误差。

这个误差会随着时间的延长逐步增加，无法输出正确的角度信号。最终误差将会越累计越大，导致输出的到的值越来越偏离现实

回到数据本身

陀螺仪一般都不会直接给你输出一个单位为度 / 秒的值（除非它是个特殊的数字陀螺仪）。在 MPU-6050 传感器中，就像读取加速度数据一样，你会得到一个经过内置 ADC 转换后得到的数字量，单位为 。参考对加速度数据的处理，我们同样得到：

其中：

• ， ：这两个值是陀螺仪数据，它们分别代表矢量 R 的投影在 XZ 和 YZ 平面内里的转角，也可等价的说，旋转可分解为单独绕 Y 和 X 轴的运动

• ： 陀螺仪零偏值，换句话说，它是陀螺仪静止不动时的输出值。理论上，陀螺仪静止不动时，应该输出为 0 的值，但是受制造工艺、外部因素的影响，陀螺仪静止不动时输出一个比较小的随机的不为 0 的值，我们称之为零偏值

• Sensitivity – 陀螺仪的灵敏度，单位 ，它的意思就是如果旋转速度增加 ，陀螺仪的输出就会增加多少 LSB。灵敏度在规格书中可以查到的

数据的融合

测量倾角

目前阶段，通过简单的互补滤波融合这两个传感器的数据（当然是倾角）就可以对角度信息进行校正，当然以后你也可以使用卡尔曼滤波

互补滤波

它的核心公式如下：

其中：

• 为经过互补滤波后得到的角度
• 为陀螺仪部分得到的角速度
• 为加速度传感器部分通过反正切函数 再转换单位后的角度
• 为滤波器的运行周期
• 0.98 和 0.02 为加权系数 和

其代码实现为：

// a = tau / (tau + dt)  
// acc = 加速度传感器数据 
// gyro = 陀螺仪数据 
// dt = 运行周期       
float angle;
float a;
float ComplementaryFliter(float acc, float gyro, float dt) 
{
    a = 0.98;  
    angle = a * (angle + gyro * dt) + (1 - a) * (acc);  
    return angle;  
}

互补滤波的加权系数

在《The Balance Filter》中提到关于加权系数的求解公式。在这里，先设滤波器的加权系数为 ，时间常数为为 ，运行周期为 ，那么公式为：

运行周期  通常都是我们设定的。比如在程序里，我们打算让互补滤波器在  中运行 200 次，那么 

时间常数   的取值是由我们根据系统的实际滤波需求调整的，每个不同的系统的  值都不一定相同。时间常数  是“信任”陀螺仪和“信任”加速度传感器的边界值。若时间常数  取值越大，则更加“信任”陀螺仪积分，但跟随加速度传感器的速度会变慢。若时间常数取  值越小，则更加“信任”加速度传感器，但同时引入加速度传感器中更多的噪声。

通常，互补滤波器是为了得到更“纯”的融合角度，必须要“信任”陀螺仪积分多些，以削弱加速度传感器中噪声的影响

比如，互补滤波器放在  周期中循环运行，时间常数 ，那么，此时加权系数为：

函数的入口参数是加速度传感器数据、陀螺仪数据和运行周期。经过计算后，函数返回融合角度。

为了更进一步了解加权系数的作用，我们留意两个极值情况：

• 当 时，那么滤波器变成 ，失去了加速度传感器的修正效果，变成了一个纯粹的陀螺仪积分器，此时互补滤波器完全信任陀螺仪。
• 当  时，那么滤波器变成 ，此时陀螺仪完全失去了作用，融合角度直接等于加速度传感器数值，此时互补滤波器完全信任加速度传感器。

由此可见，加权系数  值的大小决定了互补滤波器是信任陀螺仪还是信任加速度传感器多一些，也直接决定了互补滤波器的效果。

当然，互补滤波器也存在缺陷：

• 初始化时不能及时跟随实际角度。这种情况，跟融合角度变量没有正确初始化和互补滤波器的时间常数取值有关。时间常数约大，陀螺仪积分比重越大，跟随加速度传感器的速度约慢，这意味着初始化时融合角度可能是不精准的。
• 陀螺仪的零漂问题。理论上，陀螺仪在静止的时候，读出来的数值应该为 0，但实际上往往不为 0，这个值被称为零偏值。陀螺仪每次上电后的零偏值是随机的。互补滤波器并不能有效地过滤掉陀螺仪的零漂。

下一小节，我们将教你把互补滤波实际应用到实际项目中去

参考

[1] 加速度计、陀螺仪的工作原理和数据融合 (opens new window)

[2] 平衡小车之家开发笔记